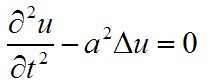波动方程或称波方程（英语：wave equation）是一种重要的偏微分方程，主要描述自然界中的各种的波动现象，包括横波和纵波，例如声波、光波和水波。波动方程抽象自声学，电磁学，和流体力学等领域。

• 波动方程简介
  
  历史上许多科学家，如达朗贝尔、欧拉、丹尼尔·伯努利和拉格朗日等在研究乐器等物体中的弦振动问题时，都对波动方程理论作出过重要贡献。
• 方程形式
  对于一个标量quantity u的波动方程的一般形式是：

  

  波动方程

  { \partial^2 u \over \partial t^2 } = c^2 \nabla^2u
  这里c通常是一个固定常数，也就是波的传播速率(对于空气中的声波大约是330米/秒, 参看音速)。对于弦的振动，这可以有很大的变化范围：在 螺旋弹簧上（slinky），它可以慢到1米/秒。但若c作为波长的函数改变，它应该用相速度代替：
  v_\mathrm = \frac{\omega}.
  注意波可能叠加到另外的运动上（例如 声波的传播在气流之类的移动媒介中）。那种情况下，标量u会包含一个 马赫因子(对于沿着流运动的波为正，对于反射波为负)。
  u = u(x,t), 是振幅,在特定位置x和特定时间t的波强度的一个测量。对于空气中的声波就是局部气压，对于振动弦就使从静止位置的位移。\nabla^2 是相对于位置变量x的拉普拉斯算子。注意u可能是一个标量或向量。
• 方程的解及条件
  对于一维标量波动方程的一般解是由达朗贝尔给出的： u(x,t) = F(x-ct) + G(x+ct) 其中F和G为任意函数，分别对应于前进行波，和后退行波。要决定F和G必须考虑两个初始条件：
  u(x,0)=f(x)
  u_{,t}(x,0)=g(x)
  这样达朗贝尔公式变成了:
  u(x,t) = \frac{f(x-ct) + f(x+ct)} + \frac \int_^{x+ct} g(s) ds
  在经典的意义下，如果f(x) \in C^k并且g(x) \in C^则u(t,x) \in C^k.
  一维情况的波动方程可以用如下方法推导：想象一个质量为m的小质点的队列，互相用长度h的弹簧连接。弹簧的硬度为k :
  这里u (x)测量位于x的质点偏离平衡位置的距离。对于位于x+h的质点的运动方程是：
  m{\partial^2u(x+h,t) \over \partial t^2}= kLINK
  其中u(x)的时间依赖性变成显式的了。
• 波动方程的物理意义
  波动方程就是描述波动现象的偏微分方程，它的物理意义就太宽泛了。不过波动方程一个很重要的性质是传播速度有限（不像热传导方程）。电磁场的运动方程是波动方程这说明电磁相互作用只能以有限的速度传播（光速c），而没有瞬时的作用（即超距作用）。这是导致狭义相对论建立的一个重要思想。