牛顿法最初由艾萨克·牛顿于1736年在 Method of Fluxions 中公开提出。而事实上方法此时已经由Joseph Raphson于1690年在Analysis Aequationum中提出，与牛顿法相关的章节《流数法》在更早的1671年已经完成了。

• 原理
  把非线性函数f(x)在x = 0处展开成泰勒级数
  牛顿法

  取其线性部分，作为非线性方程f(x)=0的近似方程，则有
  f(0 )+(x-0 ) f′(0 )=0
  设f′(0 )≠0?，则其解为x = - xf(1)
  再把f(x)在x 处展开为泰勒级数，取其线性部分为f(x)=0的近似方程，若f′(x ) ≠0，则得x = - 如此继续下去，得到牛顿法的迭代公式：x = - ...(n=0,1,2,…) (2)
  例1 用牛顿法求方程f(x)=x +4x -10=0在[1,2]内一个实根，取初始近似值x =1.5。 解 ?f′(x)=3x +8x??所以迭代公式为：
  x = -... n=0,1, 2，...
  列表计算如下：
  n
  0
  1
  2
  3
  1.5
  1.3733333
  1.36526201
  1.36523001
• 运算方法

  导数法

  这里将简单介绍一下牛顿二阶导数法。对其几何意义及收敛性不作详细的叙述，读者可仿照牛顿法进行讨论。
  将f(x)在 处展开泰勒级数

  搜寻方向较近似于牛顿法

  f(x)=f( )+f′( )(x- )+ f″( )(x- ) +…
  取右端前三项近似代替f(x)，于是得f(x)=0的近似方程为
  f( )+f′( )(x- )+ f″( )(x- ) =0
  也即f( )+(x- )[f′( )+ f″( )(x- )] =0 (3)
  设其解为 .利用(1)， - =- ，代入(3)中括号内 - ,则得f( )+( - ) [f′( )+ f″( ) ] =0
  于是解出 ，得 = -
  重复以上过程得： = -
  于是得牛顿二阶导数法的迭代公式为：
  = - n=0,1,2,… (4)
  上式与牛顿法迭代公式(2)相比，利用此公式求根收敛更快，迭代次数更少。其缺点是要求f(x)的二阶导数存在。

  切线法

  这是一个由开方公式引出的：
  X(n+1)=Xn+(A/X^(k-1)-Xn)1/k (5)（n,n+1表示下角标）
  开立方公式：
  当（5）式中的K=3时就是开立方公式。
  设A = X^3,求X.称为开立方。 开立方有一个标准的公式：
  X(n+1)=Xn+(A/X^2-Xn)1/3　(n，n+1是下角标）
  例如，A=5，,即求
  5介于1的3次方;至2的3次方;之间（1的3次方=1，2的3次方=8）
  初始值X0可以取1.1，1.2，1.3，1.4，1.5，1.6，1.7，1.8，1.9，都可以。例如我们取X0 = 1.9按照公式：
  第一步：X1=1.9+（5/1.9^2;-1.9)1/3=1.7。
  即5/1.9×1.9=1.3850416，1.3850416-1.9=-0.5149584，-0.5149584×1/3=-0.1716528，1.9+(-0.1716528)=1.7。即取2位数值,，即1.7。
  第二步：X2=1.7+（5/1.7^2;-1.7)1/3=1.71。
  即5/1.7×1.7=1.73010，1.73-1.7=0.03，0.03×1/3=0.01，1.7+0.01=1.71。取3位数，比前面多取一位数。

  xn+1=xn+Δxn+1这是牛顿法的迭代公式

  第三步：X3=1.71+（5/1.71^2;-1.71)1/3=1.709.
  第四步：X4=1.709+（5/1.709^2;-1.709)1/3=1.7099
  这种方法可以自动调节，第一步与第三步取值偏大，但是计算出来以后输出值会自动转小；第二步，第四步输入值
  偏小，输出值自动转大。即5=1.7099^3;
  当然初始值X0也可以取1.1，1.2，1.3，。。。1.8，1.9中的任何一个,都是X1 = 1.7 > 。当然，我们在实际中初始值最好采用中间值，即1.5。 1.5+（5/1.5²-1.5）1/3=1.7。
  如果用这个公式开平方，只需将3改成2，2改成1。即
  X（n + 1） = Xn + (A / Xn − Xn)1 / 2 （n，n+1是下角标）
  例如，A=5：
  5介于2的平方至3的平方;之间。我们取初始值2.1，2.2，2.3，2.4，2.5，2.6，2.7，2.8，2.9都可以，我们最好取 中间值2.5。 第一步：2.5+（5/2.5-2.5)1/2=2.2；
  即5/2.5=2，2-2.5=-0.5，-0.5×1/2=-0.25，2.5+(-0.25)=2.25，取2位数2.2。
  第二步：2.2+(5/2.2-2.2)1/2=2.23；
  即5/2.2=2.272，2.272-2.2=-0.072，-0.072×1/2=-0.036，2.2+0.036=2.23。取3位数。
  第三步：2.23+(5/2.23-2.23)1/2=2.236。
  即5/2.23=2.242,2.242-2.23=0.012,0.012×1/2=0.006,2.23+0.006=2.236.
  每一步多取一位数。这个方法又叫反馈开方，即使你输入一个错误的数值，也没有关系，输出值会自动调节，接近准确值。
  详见百度文库《开立方公式》《从二项式定理开方到切线法》。

  切线法

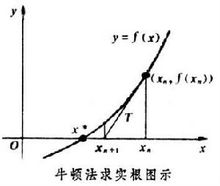
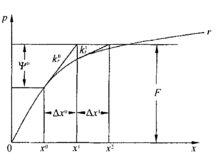
  方程f(x)=0的根就是曲线y=f(x)与x轴交点的横坐标x*，当初始近似值x0选取后，过( x0,f(x0))作切线，其切线方程为：y- f(x0)=f′(x0)(x-x0)
  它与x轴交点的横坐标为x
  一般地，设 是x*的第n次近似值，过( x,f(x))作y=f(x)的切线，其切线与x轴交点的横坐标为：x = - 即用切线与x轴交点的横坐标近似代
  曲线与x轴交点的横坐标，如图2-4。
  2-4
  牛顿法正因为有此明显的几何意义，所以也叫切线法。
• 主要案例
  定理：
  设f(x)在[a,b]满足
  (1) f(a)·f(b)<0
  (2) f(x)∈[a,b]，f′(x),f″(x)均存在，且f′(x)与f″( x)的符号均保持不变。
  (3) f(x)·f″(x)>0, x∈[a,b] 则方程f(x)=0在[a,b]上有且只有一个实根，由牛顿法迭代公式计算得到的近似解序列{ }收敛于方程 f(x)=0 的根 x*。
  由方程f(x)=0得到的牛顿迭代形式：
  x=x- =1- = 由于f(x*)=0，所以当f′(x*)≠0时， (x* )= 0，牛顿法至少是二阶收敛的，即牛顿法在单根附近至少是二阶收敛的，在重根附近是线性收敛的。
  牛顿法收敛很快，而且可求复根，缺点是对重根收敛较慢，要求函数的一阶导数存在。