假定：种群在无限环境中生长，不受资源，空间条件的限制，增长是无限的；

世代不相重叠（假如寿命只有一年，一年只有一个繁殖季），其增长是不连续的；

种群无迁入和迁出；

种群无年龄结构。

则Nt=λ^t*N0

方程中N0表示初始种群数量，λ表示周限增装率，t表示时间（t个时间单位），Nt表示t个时间单位后种群数量。这一方程表明种群呈指数式或几何式增长。

当λ>1，种群上升；当λ=1，种群稳定；当0<λ<1，种群下降；当λ=0，种群无繁殖，且在一代中死亡。

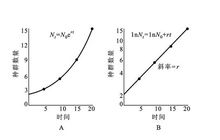
假定：世代重叠（生物一生有多个繁殖季），增长是连续的；

种群在无限环境中生长，不受资源，空间条件的限制，增长是无限的；

种群无迁入和迁出；

种群无年龄结构。

则对于无限环境中瞬时增长率r恒定的种群，则种群仍表现为指数增长，即d*N/d*t=r*N；

其积分式为Nt=N0*e^（r*t）

式中N0，Nt，t的定义与世代不相重叠种群的离散增长中的定义相同，e为自然对数底（=2.718），d*N/d*t为种群瞬时数量变化。其中Nt=N0*e^（r*t）类似于Nt=λ^t*N0，只是e^r取代了λ。

当λ值较大时，若以种群Nt对时间t作图，种群增长曲线呈“J”型，若以IgNt对时间t作图，则成为直线型

当r>0，种群增长；r=0，种群稳定；r<0，种群下降；r=—∞，种群灭亡